La référence de tension Bandgap est un des schémas électroniques les plus utilisés dans l'électronique moderne. Mais pourtant reste assez méconnu alors qu'on la trouve (dans son principe) un peu partout dans les circuits intégrés, et notamment dans tous les régulateurs de tensions (78XX, 79XX, TL431, LM317 ...).

Dans cet article, je vais vous présenter le circuit bandgap de Robert Widlar qui a inspiré la plupart des circuits Bandgap actuels.

1) Concepts des références de tensions dans les circuits intégrés

Un des besoins de la microélectronique est de disposer d'une référence de tension au sein des circuits intégrés. Et notamment, on trouve ces références dans les régulateurs de tension.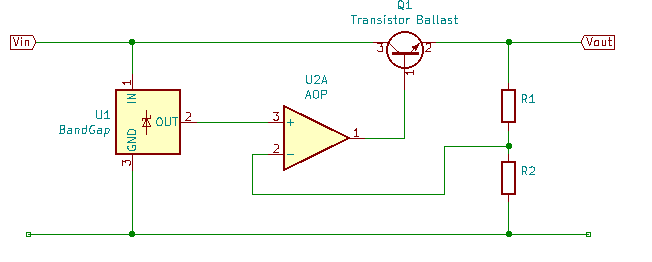



L'idéal est que cette référence soit réalisée avec des semiconducteurs à base de silicium afin de réduire les problématiques d'espace et de coûts. Donc de réaliser cette référence de tension avec des transistors bipolaire et des résistances.

La principale difficulté est que le transistor bipolaire est sensible aux variations de température. En particulier, la tension base-émetteur d'un transistor BJT est une fonction linéaire de la température absolue et présente un coefficient de température d'environ -2mV/°C.



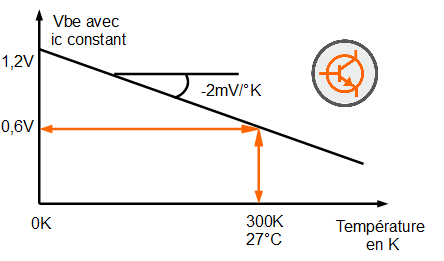
Ceci peut paraitre anodin, mais ça ne l'est pas vraiment quand on sait qu'un régulateur de tension en circuit intégré peut avoir des variations de température significatives. Il faut donc que la référence soit insensible aux changements de température, ce qui en soit est un vrai défi. Alors comment faire?

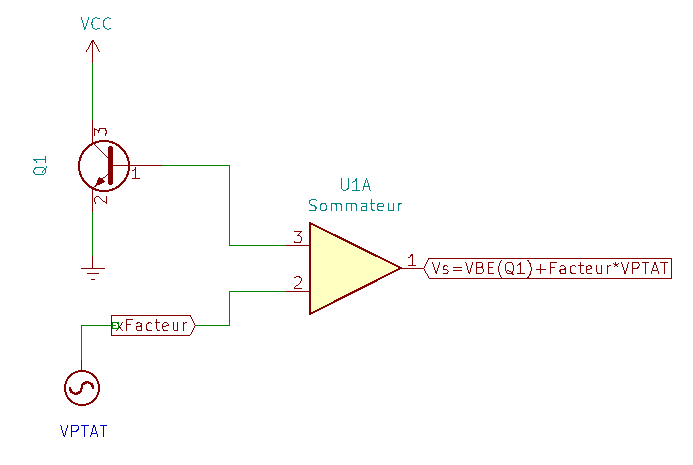
Il faudrait être capable de disposer d'un générateur de tension positive constant avec la température. Dans le jargon, on appelle ceci un proportional to absolute temperature (PTAT). Il suffira alors de l'adapter à la perte des -2mV/° et de l'ajouter pour obtenir une tension constante et indépendante des fluctuations de température.

2) Référence de tension Bandgap de WIDLAR

Robert WIDLAR est un ingénieur spécialisé dans la conception des circuits intégrés. Il a conçu de nombreux circuits intégrés dont le premier amplificateur opérationnel (AOP) avec David TALBERT. Parmi ses conceptions, il y a la première référence de tension de Bandgap qui donne le principe de la plupart des références intégrées actuelles. Véritable pionnier, il a énormément contribué aux grands principes de la microélectronique d'aujourd'hui.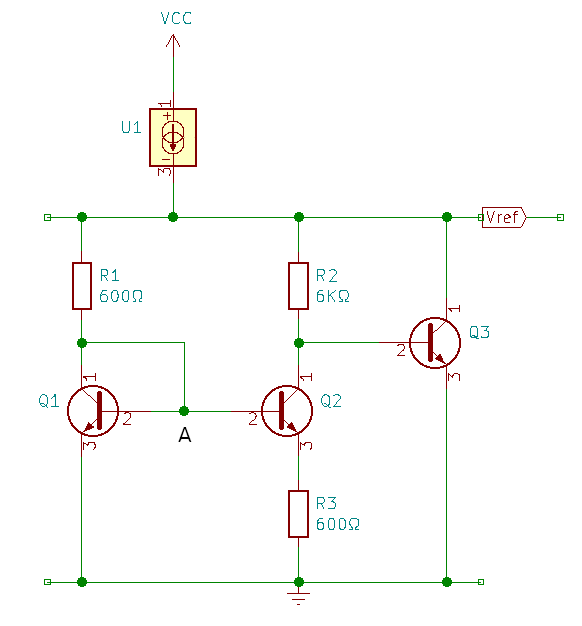



Ci-dessus, vous trouverez le schéma de R. WIDLAR. Alors, comment fonctionne t'il? Passons à l'analyse mathématique (pour les allergiques, passez à la synthèse directement).

En prémices, je rappelle que pour un transistor bipolaire, le courant de collecteur est tel que Ic=Is * exp(Vbe/VT) avec VT=KT/q où K=1.38*10^-23 est la constante de Boltzmann et q=1.6*10^-19 pour la charge d'un électron.

Partie 1 : Si l'on considère la tension au point A:
VA=Vbe1=Vbe2+VR3 (Vbe1 pour Q1, Vbe2 pour Q2 et VR3 la tension aux bornes de R3)
VR3=Vbe1-Vbe2=ΔVbe (Relation 1)

Donc la tension aux bornes de R3 représente la différence des tensions base-émetteur de Q1 et Q2.

Partie 2 : Si on considère, les courants de collecteurs de Q1 et Q2 :
Ic1=Is*exp(Vbe/VT)
Ic2=Is*exp(Vbe/VT)

Et si on s'intéresse à Ic1/Ic2 :
Ic1/Ic2= exp(Vbe1/VT)/exp(Vbe2/VT)
Ic1/Ic2= exp(Vbe1-Vbe2/VT)
Ln(Ic1/Ic2)= Vbe1-Vbe2/VT
Donc ΔVbe=Ln(Ic1/Ic2) * VT (Relation 2)

Partie 3 : Si on considère, les mailles de Q1 et Q3, on a :
VR1+Vbe1=VR2+Vbe3

Or les transistors Q1 et Q3 sont parfaitement égaux, en surface d'émetteur et en température, aussi Vbe1 et Vbe2 sont identiques. Donc :
VR1=VR2
R1 * Ic1 = R2 * Ic2 (on néglige les courants des bases)
Ic1/Ic2=R2/R1 (Relation 3)

Partie 4 : Si on combine les relations 1, 2 et 3 : ΔVbe=Ln(R2/R1) * VT

Et comme VT=KT/q



Et dans notre schéma : Ln(R2/R1)=Ln(10)=2.3
Donc :
ΔVbe=Ln(R2/R1) * KT/q
ΔVbe=2.3 * KT/q
ΔVbe=2.3 * 1.38*10^-23 / 1.6*10^-19 * T
ΔVbe=0.2mV * T

Etape final :
VR2=R2 * Ic3
VR2=R2 * (ΔVbe / R3)
VR2=R2/R3 * ΔVbe
VR2=10ΔVbe

La tension de référence Vref peut s'écrire selon la maille de Q3 :
Vref=Vbe3+VR2
Vref=Vbe3+2mV * T
A T=300K (27°), si Vbe=0.65V alors Vref=0.65+300 * 2 * 10^-3=1.25V



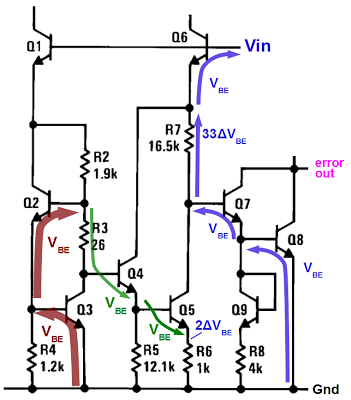
Voilà, CQFD. Maintenant, nous avons fait dans notre exemple quelques considérations pour simplifier la démonstration. Dans les faits, la variation de Vbe n'est pas complétement linéaire. Elle est plutôt concave. Aussi, il existe depuis de nombreuses adaptations de ce schéma plus sophistiquées pour prendre en compte ce phénomène. A titre d'exemple, vous trouverez ci-dessous la référence Bandgap du 7805, et son analyse : http://www.righto.com/2014/09/reverse-engineering-counterfeit-7805.html

Conclusion

Le circuit Bandgap est prévu pour un fonctionnement en micro-électronique, c'est à dire en interne des circuits intégrés. Il sera difficile (mais pas impossible) de le reproduire avec des composants discrets. D'ailleurs le cout et les performances des régulateurs de tension en circuits intégrés expliquent pourquoi ce mécanisme est assez méconnu puisqu'on ne le trouve jamais dans des circuits électroniques classiques.

L'objectif de cet article était simplement de présenter les concepts et mécanismes des références de tension Bandgap. J'espère avoir réussi?



Références :

How to Make a BANDGAP VOLTAGE REFERENCE in ONE EASY Lesson

Reverse engineering a counterfeit 7805 voltage regulator

Bandgap voltage reference

Introduction to Bandgap Voltage References

Voltage reference and bandgap circuits