L'oscillateur est à la base de l'électronique moderne, on le trouve un partout dans les circuits pour différents traitements. Le plus simple de tous est l'oscillateur LC, je vous présenterai notamment les topologies les plus communes que l'on rencontre.

Pour finir avec un peu de pratique, nous réaliserons un oscillateur haute fréquence dit de "Colpitts" pour le fun avec un transistor et quelques composants.

1) Théorie de l'oscillation LC

Commençons par un peu de théorie, en particulier pour expliquer pourquoi le circuit LC est oscillant.

Par une analyse intuitive, on comprend que le condensateur se décharge dans la bobine, qui résiste aux variations de mouvements des électrons et emmagasine de l'énergie. Cette énergie est retournée vers le condensateur par l'intermédiaire des électrons qui recharge le condensateur. Et ainsi de suite, ce phénomène se reproduit par la charge et décharge du condensateur, on obtient ainsi une oscillation.

Par une analyse physique, si on s'intéresse au schéma alors : \(u_L(t) = u_C(t) \Rightarrow L \frac{di(t)}{dt} = -\frac{1}{C} \int i(t) ~dt\)
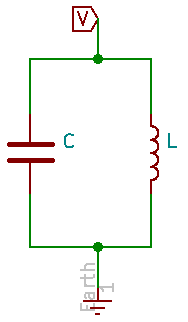
Or \(q(t) = Cu_C(t)\)
Ce qui donne donc \(\frac{dq(t)}{dt} = C \frac{du_C (t)}{dt} = - i(t)\) De plus : \(\frac{d^2q(t)}{dt^2} = - \frac{di(t)}{dt}\)
On obtient alors l'équation différentielle du second degré de la forme suivante : \(L\frac{d^2q}{dt^2} + \frac{1}{C}q = 0\)

La solution de ce type d'équation est : \(q(t) = q_m \cos (\omega_0 t + \varphi)\) avec \(\omega_0 = \sqrt{\frac{1}{LC}}\)
Et donc \(i(t) = -\frac{dq}{dt} = q_0 \omega_0 \sin \omega_0~t\)
\(u_L(t) = u_C(t) = L\frac{di}{dt} = L ~q_0 ~\omega^2_0~ \cos \omega_0 t\)

Le signal de tension du circuit LC est donc de la forme sinusoïdale avec \(\omega_0 = \sqrt{\frac{1}{LC}}\) .

A noter que nous sommes dans un régime d'oscillation idéale sans perte de résistance, ce qui est purement théorique. Evidemment, le circuit dispose d'une résistance même faible, ce qui a pour effet de donner un signal qui s'atténue en fonction du temps, on appelle ce phénomène l'ondulation amortie.



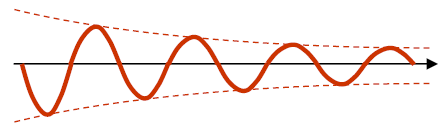
Il est nécessaire d'apporter un peu d'énergie pour maintenir une oscillation stable.

2) Les différentes topologies d'oscillateurs LC

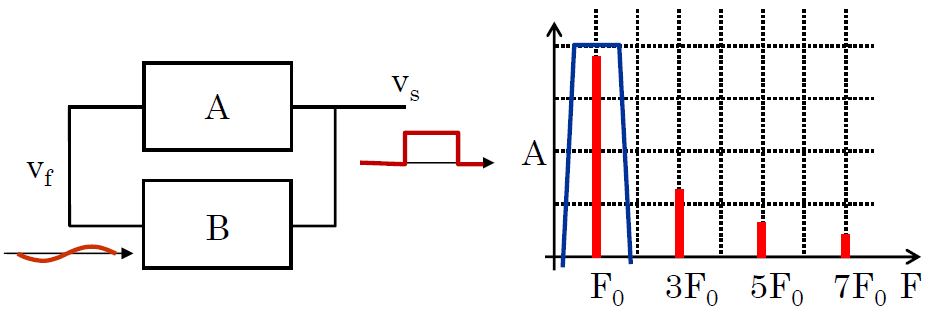
On théorise les oscillateurs selon le schème ci-dessous.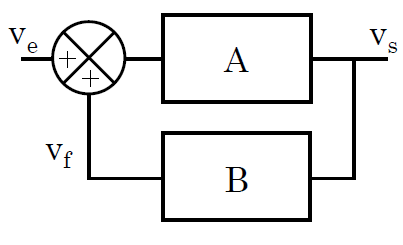

Dans ce schéma, un oscillateur est composé d'un amplificateur A et d'une boucle de rétroaction B. Les signaux Ve et Vs sont en phase.

Vs=A(Ve+Vf)=A(V+BVs)
Et donc la fonction de transfert : H=Vs/Ve=A/(1-AB)

Le système oscille si on respecte les deux critères de Barkhausen:

Le déphasage de la boucle est nulle (ou 360°) ;

|AB|=1, le gain totale de boucle est de 1.

Dans ce cas, l'oscillation est constante. L'amplificateur A compense la perte afin de réguler le niveau du signal.



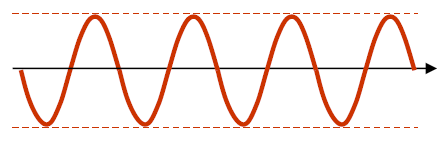
Le bloc B dans la boucle de retour peut prendre différentes formes. Vous trouverez ci-dessous les principales qui correspondent à chaque fois à un type d'oscillateur spécifique.

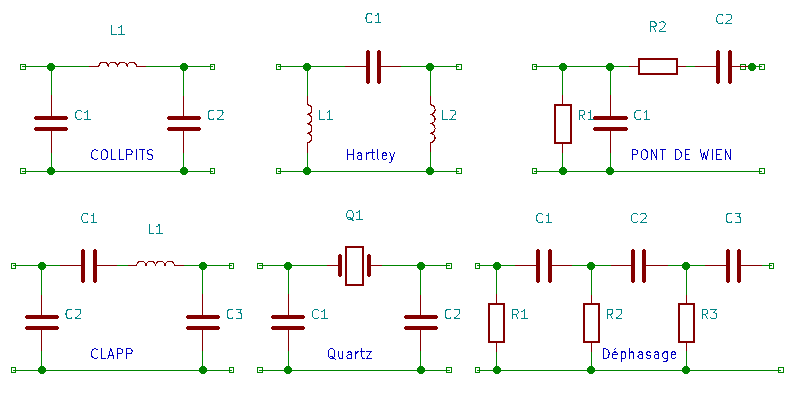
Les principes théoriques de ces oscillateurs sont assez diversifiés. Il y a notamment certains oscillateurs qui présentent une saturation en sortie. Donc un signal carré. Or un signal carré est une somme des harmoniques impaires, tel que :


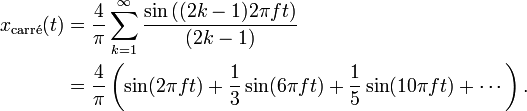
Il suffit alors d'appliquer un filtre au signal carré pour récupérer une harmonique. En effet, les blocs de rétroaction B sont des filtres qui ont cette fonction pour certains oscillateurs.

3) Pratique avec l'oscillateur Colpitts

Il existe plusieurs implémentations de l'oscillateur Collpits avec un transistor, notamment deux qui se distinguent : Oscillateur Colpitts à Emetteur commun et celui base commune.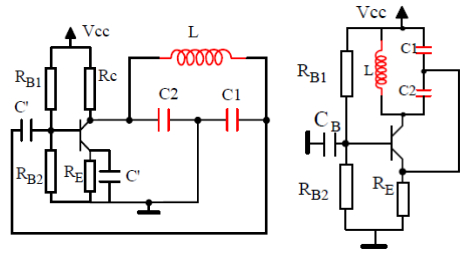


J'ai réalisé le schéma ci dessous, dit à base commune, sur une plaquette d'expérimentation en évitant d'utiliser les cordons Dupont.


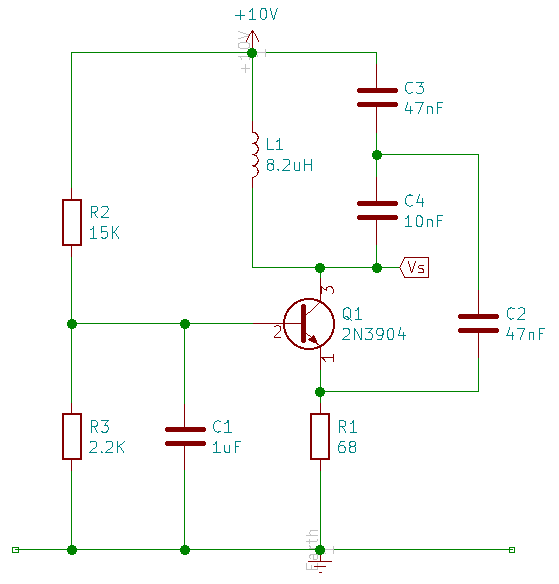
Le signal de sortie est assez propre, on observe une sinusoïde comme attendu.


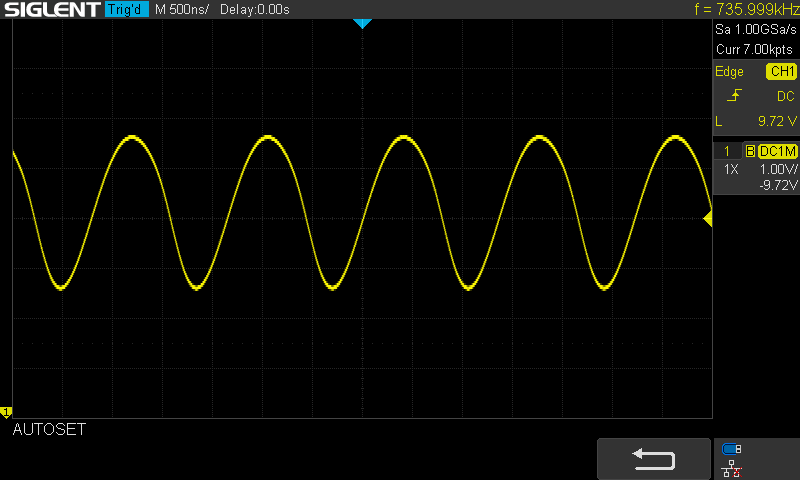
Au niveau du spectre, la FFT permet l'affichage ci-dessous.


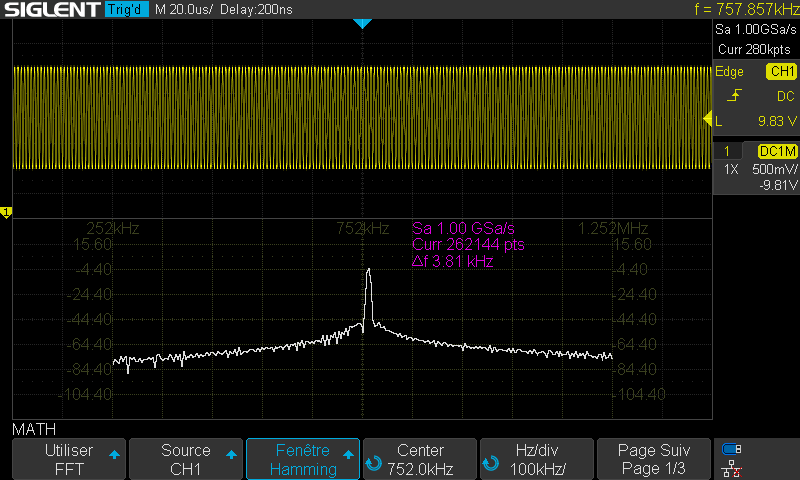
Le montage étant réalisé sur breadboard, pas forcément de bonne qualité, les connections apportent pas mal de capacités parasites. Néanmoins, à quelques dizaines de Khz prés, on observe l'harmonique fondamentale théorique qui se détache bien du reste du spectre.

Conclusion

Voilà quelques notions sur l'oscillateur LC, et l'exemple est assez plaisant à réaliser. Si vous souhaitez aller plus loin, je mets ci-dessous quelques documents intéressants.

Références :

Les oscillateurs par JP Muller

Des oscillateurs à la radio par P Masson (super documentation!)

Généralités sur les oscillateurs par Mr BEN CHEHIDA R et Mr MABROUK I

Théorie des oscillateurs électroniques par Christian G.H. MAENNEL

Radiocommunications - oscillateurs par Joël Redoutey